Irányított gráfok és nem teljesen kitöltött páros összehasonlítás mátrixok: egy axiomatikus eredmény

A többszempontú döntési problémák megoldásának egyik jól bevált megközelítése a páros összehasonlítások használata. Ezek száma azonban négyzetesen növekszik az alternatívák számával, ezért sokszor nincs lehetőség minden páros összehasonlítás összegyűjtésére, a hiányzó értékeket a meglevők alapján kell becsülni. Csató László, a Mérnöki és Üzleti Intelligencia KutatólaboratóriumOperációkutatás és Döntési Rendszerek Kutatócsoport tudományos munkatársa az e célra javasolt kitöltési eljárásokkal szemben fogalmazott meg egy észszerű követelményt. Majd megmutatta, hogy a nemrég javasolt, az inkonzisztenciát lexikografikusan minimalizáló eljárás – a legnépszerűbb kitöltési módszerektől eltérően – teljesíti ezt a tulajdonságot. A kutatást összegző, szabadon hozzáférhető cikk az International Journal of Approximate Reasoning folyóirat hasábjain jelent meg, „How to choose a completion method for pairwise comparison matrices with missing entries: An axiomatic result” címmel.

A többszempontú döntési problémák során a páros összehasonlításokat gyakran használják a szempontsúlyok meghatározására és az alternatívák értékelésére. Az így kapott kvantitatív értékeléseket egy mátrixba rendezve a feladat a megadott értékekhez jól illeszkedő súlyvektor meghatározására egyszerűsödik.

Ennek során két probléma merül fel. Egyrészt, a közvetlen és közvetett, más alternatívákon keresztül történő összehasonlítások eredménye jellemzően nem azonos: ha például az A alternatíva kétszer jobb B-nél, B pedig háromszor jobb C-nél, akkor A nem feltétlenül lesz hatszor jobb C-nél. A páros összehasonlítások tehát inkonzisztensek lehetnek, ennek mértéke különböző inkonzisztencia indexekkel számszerűsíthető.

Másrészt, a páros összehasonlítások száma az alternatívákénak négyzetes függvénye: három alternatíva esetén három, négynél hat, ötnél 10, nyolcnál viszont már 28 páros összehasonlítás elvégzése szükséges. Ezért egyre elterjedtebb a nem teljesen kitöltött (hiányos) páros összehasonlítás mátrixok alkalmazása. Ilyen esetekben a hiányzó értékeket a meglevők alapján becsülik meg, jellemzően az inkonzisztencia szintjének minimalizálásával.

A kutatási kérdés

Az inkonzisztencia számszerűsítése azonban csak három alternatíva esetén egyszerű, ennél nagyobb méretben már nincs egyértelműen preferált aggregálási módszer. Ennek megfelelően az irodalomban többtucatnyi inkonzisztencia indexet javasoltak, ami legalább ennyi lehetőséget jelent a hiányzó páros összehasonlítások megadására. Hogyan válasszon a döntéshozó ezek közül?

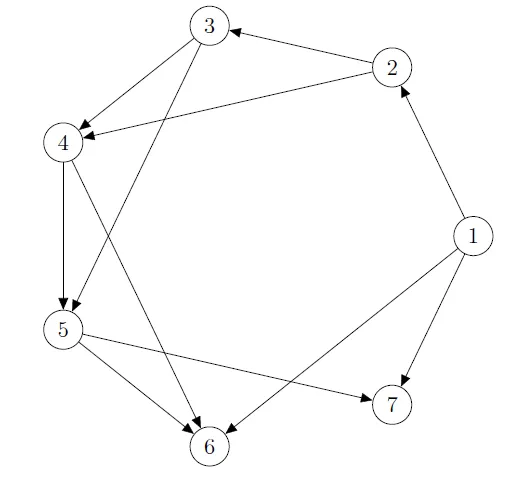
Hasonló módszertanválasztási kérdések esetén jól alkalmazható a szavazáselméletből – például az Arrow-tétel kapcsán – ismert axiomatikus megközelítés: néhány észszerű elméleti tulajdonság megfogalmazása után ellenőrizhető, vajon az egyes módszerek közül melyek teljesítik ezeket a követelményeket. Jelen esetben abból indulunk ki, hogy a döntéshozó preferenciái leírhatók egy körmentes irányított gráffal, ennek megfelelően adja meg a páros összehasonlítás mátrix értékeit. Azt kell megvizsgálni, vajon az ebből a nem teljesen kitöltött mátrixból adódó súlyvektor kompatibilis-e a körmentes irányított gráfhoz tartozó rangsorokkal, vagy bizonyos esetekben mindegyikkel ellentmondásba kerül.

A fő eredmény

Az axióma nem olyan „ártatlan”, mint elsőre gondolnánk: Csató László és Rónyai Lajos (BME, SZTAKI) egy 2016-os eredménye szerint a két legnépszerűbb kitöltési és súlyvektor meghatározási eljárás, a logaritmikus legkisebb négyzetek módszere és a sajátvektor módszer sem teljesíti azt. Ezzel szemben a tavaly javasolt, az alternatívahármasok (triádok) inkonzisztenciáit lexikografikusan minimalizáló kitöltés már olyan páros összehasonlítás mátrixot eredményez, amiből egy jól viselkedő súlyozási módszer a körmentes irányított gráffal összeegyeztethető rangsort ad. Ez a tétel meglehetősen erős érvet szolgáltat a lexikografikus minimalizálás választása mellett. A cikkben vizsgált axióma egyúttal a nem teljesen kitöltött páros összehasonlítás mátrixok vizsgálatának fontos kiindulópontjává válhat.